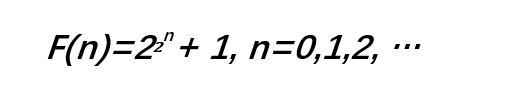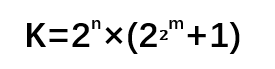智能时代,需要像“高斯”这么会算的数学王子

7+17+27+37+……+447=?
13+26+39+52+……+5200=?
……
看到上面这一串数学题,我的思绪顿时就回到了高考前冲刺的数学课堂上。在那个让人昏昏沉沉的夏日午后,数学老师大声说着:“考试时别紧张,一定是先易后难”,但是我心里却在默念:“离下课还有9,7,5,3,1……秒”。
在1787年,10岁的高斯(Johann Carl Friedrich Gauss)也碰到了这类问题,不过当时老师问的看起来好像要更难一点:
81297+81495+81693+…+100899……(也有“计算1到100的和”这个版本)
在现在看来,这不就是一个等差数列的求和问题吗?但是要知道在200多年前还没有等差数列这个概念,不过高斯很快就在小石板上写下了答案,全场选手和裁判都惊呆了,然而这只是高斯数学生涯的开始。

约翰·卡尔·弗里德里希·高斯 | Wikipedia
数学爱好者的旅行箱用来干嘛?
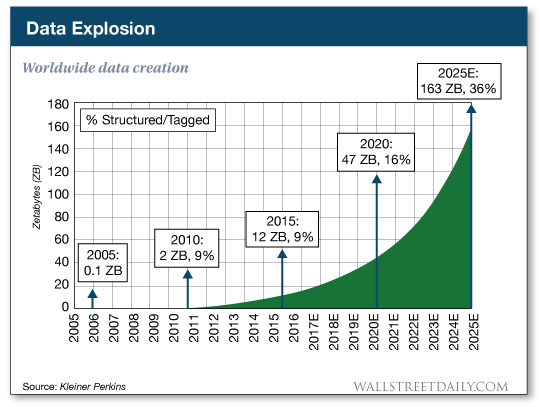
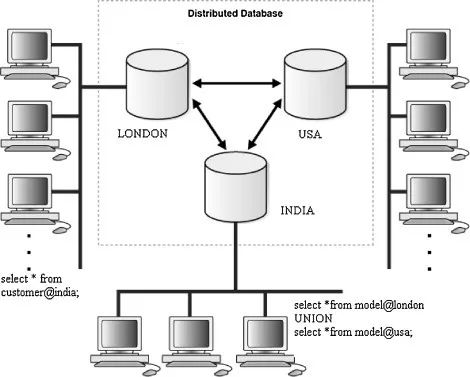
大概都用来装草稿纸吧 高斯的一生成就无数,他推演出了(地球人都知道的)等差数列求和公式,还独立给出四种证明的代数基本定理,可是他的墓碑上并没有提到这两点,却只是篆刻了一个正十七边形。这是高斯在尺规作图领域中的一个大神级操作——用尺规作出正十七边形。陈述起来过于繁琐,请参考下面一镜到底的演示。 用尺规作正十七边形 | Wikimedia Commons 可怕的是,高斯不仅告诉了大家这个图怎么画,还证明了用尺规作图做出正多边形需要满足的条件就是:边数目必须是2的非负整数次方和不同的费马素数的积。哎等等,费马素数又是个啥? 费马也是一位国服排名前几的大数学家,但“费马素数”却是他为数不多翻船点。费马在1640年提出,所有如下数列算出的都是素数(质数)。这个数列的前 5 个数的值分别是3,5,17,257和65537——确实都是素数。不过欧拉却指出第六个数F(5) = 641×6700417却不是一个素数,后来随着计算机技术的发展,人们发现从F(5)开始,往后就再也没有素数了。但谁也想不到的是,费马的这个失误意外地和尺规作图联系到了一起。 根据高斯的结论,正多边形边数只有在满足以下条件: 其中n,m= 0,1,2,… 时才能通过尺规画出来。将正n边形的每一条边对应的圆弧二等分,我们可以轻易地做出正2n边形。这是一个延绵了两千多年的尺规作图难题,阿基米德和牛顿都没能解决,高斯给出了一个肯定的解答。在高斯之后,也有人陆续给出了正257边形和正65537边形的尺规作图过程。其中正 65537 边形的作图过程十分繁琐,只是讲做图方法的计算手稿就有 200 页,完整的过程更是装满了一个皮箱,现在被收藏于高斯的母校哥廷根大学。 浩如烟海的信息运算,人脑就不参与了吧 多边形的边数在变多,计算的草稿纸也摞得越来越高,正如这个世界正在呈指数增长的信息洪流——20世纪60年代信息总量约72亿字节,80年代信息总量约500万亿字节 ……而到了2025年,有机构预计全球的数据量将达到1630万万亿字节。数据爆炸就是当下你我身处时代的标配tag。 数据的爆炸的曲线像不像高考数学最后一道大题 | Investing.com 举栗来说,如果只是八卦某同事最近三天一共发了多少条朋友圈吐槽996加班,一共加班了多长时间,还是可以很容易得到答案的。但是在这样一个信息爆炸的时代,如果老板让你的计算稍微升级,要求你计算出最近一年食堂饭菜的难吃程度和全公司同事吐槽加班次数的线性关系,可能现在你已经在敲“辞职信”的第一个字了。 这就好比当年高斯的数学运算过程,17、257甚至65537边形作图过程的计算都可能通过笔算完成,但是更大的数据介入后,人脑将不能再有效完成运算。不仅是计算结果很难得到,要想检索留下计算过程的草稿纸的难度也在不断提高,脑补一下在满满一屋子草稿纸中查找一行方程式的情形。算了算了,我宁愿这是一场噩梦。 虽然有人说大脑像计算机一样运转,因为大脑本身是硬件,思想是软件。但是在海量的运算要求下,即使有了高斯的大脑也不太好用。因为人脑并不“存储”单词和语法;不创建视觉刺激的“表征”并将它们“存储”在内存缓冲区后“传输”到硬盘里;不从寄存器中“检索”信息图片或单词;也并不像二进制一样进行数据分析和处理。就算现在给你教授一整套猎鹰9号的设计方案,但是听完之后你(可能)也不能立刻完美地将其复刻出来,因为人脑只是一直在对外界刺激作出经验性的反射和回应。 人脑神经元结构 | Wikipedia 所以计算机的出现充分解决了人脑的压力。现在在美国一家过滤器公司的1948年的“电脑” IBM 402还在吭哧吭哧地为会计做账,记录长串的数字,加和运算,打印详细的书面报告。在某种程度上,你可以把它看成一个1.36吨的电子制表机器。虽然这只是一台极其简单的计算机,但它和它的“后代”极大地推动了信息时代的进步。 在402上使用的穿孔卡片计算数据 | Wikipedia 如果现在全世界都在用这样的老式卡片储存数据和数据运算,那可能文件柜厂商就一夜暴富了。不过,随着社会的发展,数据量急剧增长,数据库(Database)的出现帮人们保存了大量的数据也摆脱了老式卡片存储的弊端,也能更好的利用这些数据资源。 未来的数据库不仅要大,还要更聪明 2016年,李世乭对AlphaGo的五番棋结束了,人类以1:4败给了AI。AlphaGo的“努力程度”让人咂舌,它每天可以和自己下数百万盘棋,而国际围棋联盟估计全世界的围棋棋手大约也只有四千万,而AlphaGo产生新对局的能力可能已经逼近甚至超过所有人类的总和。随着它计算性能的提升和其他人工智能的兴起,迟早有一天,绝大多数曾存在过的棋局都会出自程序之手。庞大且智能的数据库分类储存了海量的招式和棋路,它们是这些电脑棋手的最强大脑。 李世乭对AlphaGo | Wikimedia Commons 事实上,学术成果的普遍提升也与数据库技术的进步密不可分。以古生物专业为例,每一年专家们都会基于化石发现发表众多学术论文,在其中提出新的分类学观点,这些信息非常重要,但也非常零散。如果要得到全景式的信息图表,就得人工把这些散落在原始论文中的信息一点点提取出来,放在一个数据库里。但是每年的论文都会增加,手动录入的话可能要做到退休。于是威斯康辛大学麦迪逊分校开发了一套全新的学术数据库系统,它可以从浩如烟海的科学文献中检索信息并进行数据分类,准确率达到了92%。 多台计算机能同时访问一个数据库 | 图虫 除了人工智能机器人和学术研究,数据库的应用还将辐射到更加广阔的商业应用场景。对于企业的商业化运营来说,客户、销售、供应商等上下游的信息是一笔巨大的宝贵财富,完美处理分析这些信息,将构建出一个全面的联动场景供企业参考。 分布式数据库的概念 | tutorialride 智能时代数据量更大、数据类型更多,全靠人工调优和运维已经越来越困难,数据库也要变得更加智能,能自运维,自管理,遇到故障自愈。基于对金融、政府和大企业等行业客户的理解,华为就创新地把人工智能技术注入到了其分布式数据库GaussDB业界首款AI-Native数据库自调优自诊断自愈自运维 基于最优化理论,GaussDB首创了基于深度强化学习的自调优算法60% 企业的日常经营离不开对数据的频繁、海量访问,一家银行的一个普通的金融产品就能拥有20万+的客户群。如何适应多场景的高效数据使用需求和及时故障自查,将是数据库面临的极大挑战。 图片 | 图虫 华为GaussDB在数据处理场景,独创了超并行计算架构48%数据零丢失、故障恢复时间小于 1 秒 GaussDB支持本地部署私有云公有云 高斯用大脑将数学的书本向后翻了无数页,而数据库的进步将书写新的时代篇章。还记得前不久拍摄的模糊的黑洞照片吗?仅原始数据占用了5PB的容量,数据的整理和分析也相当费劲。 存储黑洞照片信息的物理数据库 | extremetech 在未来,构建万物互联的智能世界将更加依靠庞大的数据运算、存储和传输。华为不仅在5G技术方面取得了极大的科研成果,让数据传输坐上了火箭,在GaussDB数据库方面进行的进一步研究也将继续引领数据库新架构的发展,带来的高性能产品也将加速产业的进步。其实华为早在2011年硬件+软件+生态 在5年、10年后,世界对数据处理的能力将更快、更强,那时我们的生活又将发生什么改变呢?让科技慢慢告诉我们答案吧。